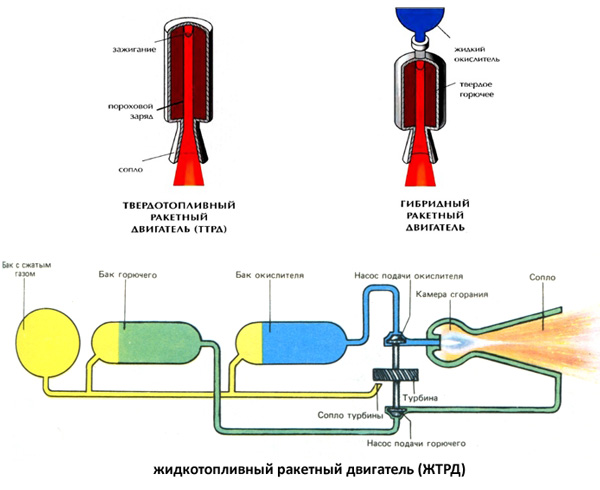
Тяга самолета. тяга двигателя самолета. тяга реактивного двигателя

Самые мощные реактивные двигатели в мире

Тяга реактивного двигателя самолета

Сила тяги двигателя, или его движущая сила, равноценна всем силам давления воздуха на внутреннюю поверхность силовой установки. Тяга некоторых видов реактивных двигателей зависит от скорости и высоты полета. Для вычисления силы тяги реактивного двигателя часто приходится определять тягу на конкретной высоте, у земли, на взлете и во время какой-либо скорости. Для ЖРД сила тяги равноценна произведению массы исходящих газов на скорость, с которой они вылетают из сопла двигателя.

Для ВРД (воздушно-реактивный двигатель) сила тяги измеряется как результат массы газов на разность скоростей, а именно скорости воздушной струи, выходящей из сопла двигателя, и скорости поступающего воздуха в двигатель. Проще говоря, данная скорость уравнивается к скорости полета самолета с реактивным двигателем. Тяга ВРД обычно измеряется в тоннах или килограммах. Важным качественным показателем ВРД является его удельная тяга. Для турбореактивного двигателя – тяга, отнесенная к конкретной единице веса воздуха, который проходит через двигатель в секунду. Этот показатель позволяет понять, насколько высока эффективность эксплуатации воздуха в двигателе для образования тяги. Удельная тяга измеряется в килограммах тяги на 1 кг воздуха, расходуемого за секунду. В некоторых случаях применяется другой показатель, который также называется удельной тягой, показывающей отношение количества топлива, которое расходуется, к силе тяги за секунду. Естественно, что чем выше показатель удельной тяги ВРД, тем меньше поперечный вес и размеры самого двигателя.

Показатель полетной или тяговой мощности – это сила, которая задействует реактивный двигатель при конкретной скорости полета. Как правило, измеряется в лошадиных силах. Величина лобовой тяги говорит о степени конструктивного оптимума реактивного двигателя. Лобовая тяга – это отношение наибольшего показателя площади поперечного сечения к тяге. Лобовая тяга равна тяге, в кг поделенной на площадь в метрах квадратных.

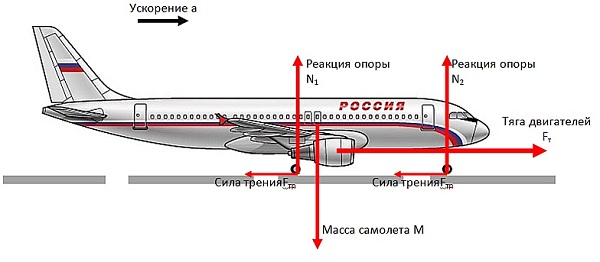
В мировой авиации наиболее ценится тот двигатель, который обладает высокой лобовой тягой.

Чем совершеннее ВРД в конструктивном отношении, тем меньший показатель его удельного веса, а именно общий вес двигателя вместе с приборами и обслуживающими агрегатами, поделенный на величину собственной тяги.

Реактивные двигатели, как и тепловые вообще, отличаются друг от друга не только по мощности, весу, тяге и другим показателям. При оценивании ВРД огромную роль играют параметры, которые зависят от собственной экономичности, а именно от КПД (коэффициент полезного действия). Среди данных показателей главным считается удаленный расход топлива на конкретную единицу тяги. Он выражается в килограммах топлива, которое расходуется за час на образование одного килограмма тяги.

Источник

Величина реактивной тяги

Формула при отсутствии внешних сил

Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.

F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}, где

mp{\displaystyle m_{p}} — масса ракеты

a→{\displaystyle {\vec {a}}} — её ускорение

u→{\displaystyle {\vec {u}}} — скорость истечения газов

ΔmtΔt{\displaystyle {\frac {\Delta m_{t}}{\Delta t}}} — расход массы топлива в единицу времени

Поскольку скорость истечения продуктов сгорания (рабочего тела) определяется физико-химическими свойствами компонентов топлива и конструктивными особенностями двигателя, являясь постоянной величиной при не очень больших изменениях режима работы реактивного двигателя, то величина реактивной силы определяется в основном массовым секундным расходом топлива.

Доказательство

До начала работы двигателей импульс ракеты и горючего был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю:
mp⋅Δv→+Δmt⋅u→={\displaystyle m_{p}\cdot \Delta {\vec {v}}+\Delta m_{t}\cdot {\vec {u}}=0}, где

Δv→{\displaystyle \Delta {\vec {v}}} — изменение скорости ракеты

mp⋅Δv→=−Δmt⋅u→{\displaystyle m_{p}\cdot \Delta {\vec {v}}=-\Delta m_{t}\cdot {\vec {u}}}

Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:

mp⋅Δv→Δt=−ΔmtΔt⋅u→{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}=-{\frac {\Delta m_{t}}{\Delta t}}\cdot {\vec {u}}}

Произведение массы ракеты m на ускорение её движения a по определению равно силе, вызывающей это ускорение:

F→p=mp⋅a→=−u→⋅ΔmtΔt{\displaystyle {\vec {F}}_{p}=m_{p}\cdot {\vec {a}}=-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}}}

Уравнение Мещерского

Если же на ракету, кроме реактивной силы F→p{\displaystyle {\vec {F}}_{p}}, действует внешняя сила F→{\displaystyle {\vec {F}}}, то уравнение динамики движения примет вид:

mp⋅Δv→Δt=F→+F→p⇔{\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+{\vec {F}}_{p}\Leftrightarrow }
mp⋅Δv→Δt=F→+(−u→⋅ΔmtΔt){\displaystyle m_{p}\cdot {\frac {\Delta {\vec {v}}}{\Delta t}}={\vec {F}}+(-{\vec {u}}\cdot {\frac {\Delta m_{t}}{\Delta t}})}

Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами F→{\displaystyle {\vec {F}}}, действующими на тело, но и реактивной силой F→p{\displaystyle {\vec {F}}_{p}}, обусловленной изменением массы движущегося тела:

a→=F→p+F→mp{\displaystyle {\vec {a}}={\frac {{\vec {F}}_{p}+{\vec {F}}}{m_{p}}}}

Формула Циолковского

Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского:

mtm=ev→u→{\displaystyle {\frac {m_{t}}{m}}=e^{\frac {\vec {v}}{\vec {u}}}}

Релятивистское обобщение этой формулы имеет вид:

mtm=(c→+v→c→−v→)c→2u→{\displaystyle {\frac {m_{t}}{m}}=\left({\frac {{\vec {c}}+{\vec {v}}}{{\vec {c}}-{\vec {v}}}}\right)^{\frac {\vec {c}}{2{\vec {u}}}}}
, где c→{\displaystyle {\vec {c}}} — скорость света.

Явление отдачи

Но научные поиски и разработки на этом не прекращались. Как всегда, на помощь пришла природа, которая, в большинстве случаев и наталкивает изобретателей на удивительные открытия.

Наблюдения за морскими жителями, такими как осьминоги, кальмары и каракатицы, привели к неожиданным результатам. Манера движения этих морских обитателей, была схожа с кратковременным толчком. Будто тело отталкивается отчего – то и продвигается вперед.

Эти наблюдения были чем-то схожи с замечаниями Гюегенса про выстрел и пушку, которые мы упоминали выше.

Таким образом, в физики появилось понятие «явление отдачи». В ходе дальнейших научных исследований было выяснено, что именно благодаря явлению отдачи происходит все движение на планете Земля: автомобиль отталкивается от земли, корабль – от воды и т.д.

Движение тел происходит благодаря передаче импульса от одного объекта другому. Для объяснения явления приведем простейший пример: вы решили толкнуть своего товарища в плечо, приложили определенную силу, в результате которой, он сдвинулся с места, но и вы испытали силу, отталкивающую вас в противоположную сторону.

Конечно, расстояние, на которое сдвинетесь вы и ваш друг, будет зависеть от ряда факторов: сколько вы весите, как сильно вы его толкнули.

Прямоточные воздушно-реактивные двигатели

Эта разновидность двигателей функционирует таким образом, что не нуждается в подвижных деталях. Воздушные массы нагнетаются в камеру сгорания непринужденным путем, благодаря торможению потоков об обтекатели входных отверстий. В дальнейшем совершается все то же, что и в обыкновенных реактивных двигателях, а именно воздушные потоки смешиваются с топливом и выходят как реактивные струи из сопел. Прямоточные воздушно-реактивные двигатели применяются в поездах, в воздушных суднах, в «беспилотниках», в ракетах, кроме того они могут устанавливаться на велосипеды или скутеры.

Источник

Что такое статическая тяга одного двигателя

Судовые двигатели

Если необходимо подчеркнуть те или иные взаимосвязи между па­раметрами, справедливые для установившихся режимов, из всего многообразия взаимосвязей (6) выбирают лишь необходимые и на их основе строят статические характеристики двигателя. Если воспользоваться для этой цели поверхностью

А (см. рис. 22), то соответствующие статические характеристики могут быть получены сечениями этой поверхности плоскостями В , С и D , парал­лельными соответствующим координатным плоскостям.

Проекции на плоскость (М; ?) сечений поверхности А плоско­стями (В), параллельными координатной плоскости (М; со), дают на плоскости (М; ?) внешнюю 1 (при h = const) и частичную 2 скоростные характеристики двигателя: М = f (?) при h = const. Проекции сечений поверхности А плоскостями (D), параллель­ными координатной плоскости (h; ?), дают на плоскости (h; ?) регулировочные характеристики 3 и 4: h = f (?) при М = const, и, наконец, проекции сечения поверхности А плоско­стями (С), параллельными координатной плоскости ( М ; h ), дают на плоскости ( М ; h) нагрузочные характеристики 5 и 6; М = f ( h ) при ? = const. Все сказанное применительно к выбран­ным трем параметрам М, ? и h можно практически повторить, если выбрать любые другие три параметра.

Таким образом, каждая точка любой статической характери­стики, т. е. каждая точка, лежащая на поверхности А и определя­емая функциональной зависимостью (6), соответствует только одному установившемуся режиму, а каждая статическая характе­ристика двигателя представляет собой последовательную совокуп­ность установившихся режимов, выраженных определенными па­раметрами при определенных условиях (например, постоянство того или иного параметра).

Один установившийся режим определяется одной точкой любой статической характери­стики, например точкой В, принадлежащей скоростной (рис. 23) или нагрузочной (рис. 24) характеристике дизеля. Этот режим соот­ветствует определенным значениям параметров М _в ; ? _в ; h _в ; g _eB ; N _eB .

Все сказанное о статических характеристиках свидетельствует о том, что их применяют для определения тех или иных статиче­ских свойств двигателя. Каждая статическая характеристика ил­люстрирует взаимосвязь параметров при установившихся режи­мах работы двигателя в определенных условиях.

Источник

Принцип работы турбовентиляторного двигателя

Турбовентиляторный двигатель технологически очень сложное изделие, но работающее по довольно простому и понятному принципу. Расскажем, о его устройстве и какие процессы и как в нём протекают. Сначала разберёмся с терминами. Слово турбовентиляторный произошло от английского turbofan, причём англоязычный мир имеет под словом turbofan абсолютно любой двухконтурный турбореактивный двигатель.

При этом они разделяют их с низкой и высокой степенью двухконтурности соответственно, а степень двухконтурности – это параметр, который показывает отношение расхода массы воздуха через внешний контур к расходу во внутреннем. Итак, неотъемлемое свойство турбовентиляторного двигателя высокая степень двухконтурности – для современных изделий от 4 и выше.

Чтобы как можно больше воздуха расходовать через внешний контур используется вентилятор большого диаметра, энергия для его вращения появляется за счёт работы внутреннего контура и в этом заключается суть работы турбовентиляторного двигателя, где с помощью вентилятора создаётся около 80% всей тяги.

Рассмотрим типичное устройство и как это работает. Турбовентиляторный двигатель имеет внешний и внутренний контуры. На входе в двигатель имеется вентилятор большого диаметра, который подаёт воздух в оба контура, устройство внутреннего контура подобно обычному турбореактивному двигателю, который состоит из компрессора, турбины, камеры сгорания и реактивного сопла.

Сначала воздух, немного увеличив давление, после вентилятора попадает в компрессор низкого давления, затем он попадает в компрессор высокого давления, который вращается в несколько раз быстрее. После прохождения обоих компрессоров, воздух, сжатый более чем в 30 раз и сильно нагретый от высокого давления попадает в камеру сгорания. Здесь он смешивается с топливом, которое подаётся с помощью форсунок и поджигается. Далее раскалённый газ с температурой около 1600 градусов и выше начинает совершать полезную работу.

Сначала он попадает в турбину высокого давления, которая заставляет вращаться, находящийся с ней на одном валу компрессор высокого давления. Затем, потратив часть энергии и снизив свою температуру, раскаленный газ попадает в турбину низкого давления, которая находится на одном валу с компрессором и вентилятором. Потеряв большую часть энергии, раскалённый газ попадает в сопло и совершает последнее полезное действие – создаёт реактивную тягу. Таков принцип работы внутреннего контура, который создаёт лишь 20% всей тяги вентиляторного двигателя.

Принцип работы внешнего контура. Турбина низкого давления, находящаяся на одном валу с вентилятором, заставляет его вращаться, воздух, пройдя через лопатки вентилятора и немного увеличив своё давление, проходит через спрямляющий аппарат, его неподвижные лопатки поворачивают поток воздуха в осевом направлении, заодно повышая его давление. Затем воздушный поток попадает в сопло, где создаётся реактивная тяга.

Вот и весь принцип работы вентиляторного двигателя. Разумеется, каждый конкретный двигатель имеет свои особенности и различия, больше всего они касаются устройства внутреннего контура, но схема исполнения всегда остаётся плюс минус одинаковой. Обычно разница заключается в количестве ступеней компрессора и турбины, также помимо двухвальной схемы используется и трёхвальная, когда вентилятор и компрессор низкого давления больше не связаны, в таком случае используется промежуточная турбина, которая вращает только компрессор низкого давления на отдельном валу.

Ещё один способ увеличения эффективности конструкции – это установка редуктора на валу, который соединяет турбину низкого давления и вентилятор, такое решение позволяет им работать на оптимальных для себя режимах. Устройство внешнего контура также может иметь заметные отличия. При относительно небольшой степени двухконтурности в двигателе может использоваться смешение потоков, где газ из обоих контуров попадает в единую камеру сгорания и покидает через общее сопло.

Но, такая схема не подходит для более габаритных двигателей с высокой степенью двухконтурности, так как масса двигателя значительно вырастет, поэтому практически во всех вентиляторных двигателях потоки не смешиваются и длина внешнего контура всегда меньше внутреннего. Вот собственно и всё – таков принцип и способы повышения эффективности работы турбовентиляторного двигателя.

Источник

Тяга двигателя

Авиация: Энциклопедия. — М.: Большая Российская Энциклопедия . Главный редактор Г.П. Свищев . 1994 .

Смотреть что такое «Тяга двигателя» в других словарях:

тяга двигателя — Результирующая всех гидродинамических сил (давления), приложенных к внутренней и наружной поверхностям двигателя в предположении, что давление на наружной поверхности равно атмосферному. Примечание. В случае турбовинтового двигателя тяга… … Политехнический терминологический толковый словарь

тяга двигателя — тяга двигателя реактивная сила, являющаяся результирующей газодинамических сил давления и трения, приложенных к внутренней и наружной поверхностям двигателя. Различают внутреннюю тягу (реактивную тягу) P результирующую всех… … Энциклопедия «Авиация»

тяга двигателя — тяга двигателя реактивная сила, являющаяся результирующей газодинамических сил давления и трения, приложенных к внутренней и наружной поверхностям двигателя. Различают внутреннюю тягу (реактивную тягу) P результирующую всех… … Энциклопедия «Авиация»

тяга (двигателя или винта) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN thrust … Справочник технического переводчика

удельная тяга двигателя — Тяга, развиваемая двигателем, отнесенная к секундному весовому расходу воздуха через двигатель … Политехнический терминологический толковый словарь

лобовая тяга двигателя — Отношение тяги двигателя к его лобовой площади. Примечание. Под лобовой площадью понимается площадь максимального сечения двигателя … Политехнический терминологический толковый словарь

тяга ЖРД (камеры ЖРД) — тяга двигателя (камеры) Равнодействующая реактивной силы ЖРД (камеры ЖРД) и сил давления окружающей среды, действующих на его (ее) внешние поверхности, за исключением сил внешнего аэродинамического сопротивления. Обозначения: тяга ЖРД R тяга… … Справочник технического переводчика

Тяга — В Викисловаре есть статья «тяга» Тяга: Тяга (авиация) сила движителя самолёта. Реактивная тяга кинетичес … Википедия

Тяга судов — по внутренним водным путям (на морях и больших озерах суда передвигаются исключительно паровою силою или под парусами, а лодки при небольших переходах на веслах) производится разнообразными способами. При движении вниз по течению пользуются силою … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

приведенная тяга — Тяга двигателя, приведенная к стандартным атмосферным условиям … Политехнический терминологический толковый словарь

Источник

Бабочка из семейства павлиноглазок (Attacus Atlas)

Гусеница до превращения в бабочку.

Роскошная ночная бабочка семейства павлиноглазок.

История создания

Как определить силу тяги двигателя. Примеры решения задач

Задача 1

Автомобиль может разгоняться до 216 км/ч. Максимальная мощность двигателя равна 96 кВт. Определите максимальную силу тяги двигателя.

Решение

Переведем киловатты в ватты, а километры в час — в метры в секунду:

\(96\;\times\;1000=96000\;Вт\)

\(\frac{216\times1000}{3600}=60\frac мс\)

\(F_т\;=\;\frac N v = \frac{96000}{60} = 1600 Н\)

Задача 2

Троллейбус весом 12 тонн за 5 секунд проезжает по горизонтальной дороге 10 метров. Сила трения равна 2,4 кН. Определите силу тяги, которую развивает двигатель.

Решение

Переведем тонны в килограммы, а килоньютоны в ньютоны:

\(12\;\times\;1000=12000\;кг\)

\(2,4\;\times\;1000=2400\;Н\)

\(F_т-\;F_{тр}=m\;\times\;a\), следовательно, \(F_т=m\times a\;+\;F_{тр}\)

Чтобы определить ускорение а, воспользуемся формулой \(s\;=\;\frac{at^2}2\)

Подставив численные значения величин, получаем:

\(a\;=\;\frac{2s}{t^2}^{}=\frac{20}{25}\;=\;0,8\)

\(F_т=\;12000\times0,8\;+\;2400\;=\;12000\;Н\;=\;12\;кН\)

Задача 3

Транспорт, весящий 4 тонны, едет в гору. Уклон — 1 метр на каждые 25 метров пути. \(\mu\) — 0,1 от силы тяжести, \(а = 0\). Определите силу тяги.

Решение

Начертим схему:

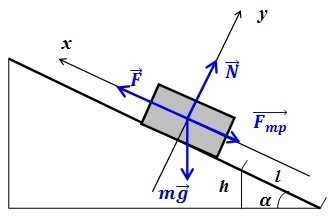
\(m\times g\;+\;N\;+\;F_{тр\;}+\;F_т\;=\;m\times a\)

Сделаем проекции на координатные оси:

\(OX: -\;mg\;\times\;\sin\alpha\;-\;F_{тр\;}+\;F_т\;=\;0\)

\(OY: N\;-\;mg\;\times\;\cos\alpha\;=\;0 => N\;=\;mg\;\times\;\cos\alpha\;\)

\(F_{тр}\;=\;\mu N\;=\;\mu mg\;\times\;\cos\alpha\)

Подставим значение \(F_{тр}\) в уравнение \(OX\) и определим \(F_т\):

\(-mg\;\times\;\sin\alpha\;-\;\mu\)

\(mg\;\times\;\cos\alpha\;+\;F_т\;=\;0\)

\(=> F\;=\;mg\;\left(\sin\alpha\;+\;\mu\;\times\;\cos\alpha\right)\)

Найдем синус и косинус \(\alpha\), подставим их в общую формулу:

\(\sin\alpha\;=\;\frac hl\;=\;\frac1{25}\)

\(\cos\alpha\;=\;\frac{\sqrt{l^{2\;}-\;h^2}}l\;\)

Таможенные ограничения

Удельная тяга и удельный импульс

Совершенство двигателя и эффективность его работы характеризуются удельной тягой. Удельной тягой называют отношение силы тяги к секундно-весовому расходу топлива.

Размерность удельной тяги будет (кг силы·сек/кг расхода) или кг·сек/кг. В зарубежной печати размерность Руд часто записывают в виде (сек). Но физический смысл значения при такой размерности теряется.

Современные модельные РДТТ имеют низкие значения удельной тяги: от 28 до 50 кг·сек/кг. Имеются и новые двигатели с удельной тягой 160 кг·сек/кг и выше, с нижним пределом давления не выше 3 кг/см 2 и сравнительно высоким удельным весом топлива — более 2 г/см 3 .

Удельная тяга показывает эффективность использования одного килограмма топлива в данном двигателе. Чем выше удельная тяга двигателя, тем меньше топлива затрачивается для получения одного и того же суммарного импульса двигателя. Значит, при одинаковом весе топлива и размерах двигателей предпочтительнее будет тот, у которого удельная тяга выше.

Задача 3. Определить вес топлива в каждом из четырех двигателей с суммарным импульсом 1 кг·сек, но с разными удельными тягами: а) Р_уд=28 кг-сек/кг; б) Р_уд=45,5 кг·сек/кг; в) Р_уд=70 кг·сек/кг; г) Р_уд=160 кг·сек/кг.

Решение. Вес топлива определим из формулы:

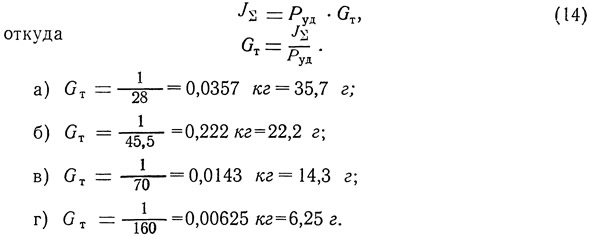
Полученные результаты наглядно показывают, что для моделей ракет выгоднее применять двигатели с более высокой удельной тягой (с целью уменьшения стартового веса модели).

Под удельным импульсом J_уд понимают отношение полного импульса тяги за время t работы двигателя к весу израсходованного за это время топлива G_T.

При постоянной тяге, т. е. при постоянном давлении в камере сгорания и работе двигателя на земле, J_уд=Р_уд.

Тяга двигателя

В ракетном двигателе струя истекающих газов формируется в сопловой, сначала сужающейся, а затем расширяющейся ча­сти камеры. Скорость текущих вдоль сопла газов постепенно на­растает, а давление соответственно падает. Возникает вопрос, где следует провести границу между отбрасываемыми газами и тем предметом, который мы будем называть ракетой.

Такое разделение можно произвести различными способами, но предпочтительным будет тот, который даст наибольшие удоб­ства для определения действующих сил.

Самое простое и очевидное — это отделить струю истекаю­щих газов по крайнему срезу сопла, а все то, что находится в пределах внешней поверхности корпуса и плоскости среза, и считать ракетой (рис. 1.3).

Отделяя мысленно, часть механической системы, мы, в со­ответствии с правилами механики, обязаны заменить действие отброшен­ной части на оставшуюся силами взаимодействия. По­скольку окружающая среда нами пока не рассматривается, мы заменяем ее действие на ракету невозмущенным атмосферным давлением р_h, распределенным по внешней поверхности. Отбра­сывая струю газов, мы также должны заменить ее действие на оставшуюся по другую сторону сечения массу давлением, которое возникает в струе на срезе сопла. Это давление принято обозначать через р_а(рис. 1.3). Оно не обязательно равно атмосферному и может быть как больше, так и меньше его.

Теперьостается условиться о том, что же следует понимать под тягой двигателя. Для ракеты это та движущая сила, перво­причину возникновения которой мы усматриваем в работе двигателя. Она обладает тем удобным свойством, что может быть непосредственно замерена на стенде (рис. 1.4).

Рис. 1.3. К выводу формулы тяги.

Для закре­пленной ракеты сила тяги уравновешивается реакцией связи R, равной тяге Р . Поэтому ускорение равно нулю, и уравнение движения для точки переменной массы (1.4) примет вид

где S_a — площадь выходного сечения сопла, а W_а— скорость истечения по­тока в этом сечении.

Рис. 1.4. Силы, действующие на закрепленную ракету.

Так как R = P, то тяга

Следует особо подчеркнуть, что под давлением р понимается исключительно барометрическое давление окружающей среды, но не истинное давление на поверхности ракеты, значение и закон распределения которого зависят от условий обтекания. Все добавочные силы, связанные со скоростью полета в атмосфере, относятся к категории аэродинамических и в выражение тяги не включаются.

Выражение для тяги на высоте h получим в окон­чательном виде:

Для стартующей с поверхности Земли ракеты тяга непрерывно возрастает от своего начального значения

(где р_о— давление у поверхности Земли) до наибольшего зна­чения, называемого пустотной тягой —

Отличие стартовой тяги от пустотной определяется площадью выходного сечения сопла и для реальных двигателей лежит в пределах 10 — 15%.

После того как введено понятие тяги, мы получаем возмож­ность написать уравнение для поступательного движения ра­кеты в обычной форме закона Ньютона (1.1):

Здесь М — текущее значение массы ракеты, а под знак суммы вынесены составляющие не рассмотренных нами пока сил, та­ких как аэродинамическое сопротивление и вес ракеты.

Итак, истекающую струю газов мы отделили от ракеты пло­скостью, проходящей через выходное сечение сопла. Но как было сказано ранее, это не единственное решение. В частности, раз­деление можно произвести по внутренней поверхности камеры, заменив действие отброшенных газов на стенки камеры некото­рым изменяющимся вдоль оси давлением р_г, приводящим к воз­никновению результирующей силы Р_г (рис. 1.5). Нетрудно дога­даться, что результирующая Р_г как раз и представляет собой пустотную тягу Р_п, из которой для определения тяги на высоте h следует вычесть произведение S_ap_h,т. е.

Таким образом, пустотная тяга представляет собой резуль­тирующую сил давления, распределенных по внутренней поверх­ности камеры. В дальнейшем мы увидим, что это давление не зависит ниот скорости полета, ни от условий окружающей среды, и поэтому пустотная тяга представляет собой одну из основных характеристик собственно самого двигателя, а не условий полета.

Часто выражение тяги в пустоте записывают в форме реактивной силы

где W_е — так называемая эффективная скорость истечения.

Рис.1.5. Распределение сил давления по поверхности ракеты и по внутренней поверхности камеры.

Из сопоставления выражений (1.6) и (1.8) следует, что эф­фективная скорость истечения

Основной особенностью эффективной скорости истечения яв­ляется то, что она не зависит от секундного расхода

р_аW_a

В заключение можно отметить, что при выводе выражения тяги нами были сделаны некоторые замаскированные упроще­ния. Ускорение

р_гМ,

Источник

Стоимость грузовика КамАЗ-43253

Галерея

Тяга самолета. тяга двигателя самолета. тяга реактивного двигателя.

Тяга – сила, выработанная двигателем. Она толкает самолет через воздушный поток. Единственное, что противостоит тяге – лобовое сопротивление. В прямолинейном горизонтально установившемся полете они относительно равны. В случае если летчик увеличивает тягу методом добавления оборотов двигателя и сохраняет постоянную высоту, тяга начинает превосходить сопротивление воздуха. Летательный аппарат (ЛА) наряду с этим ускоряется. Весьма скоро сопротивление возрастает и опять уравнивает тягу.

ЛА стабилизируется на постоянной высокой скорости. Тяга – один из самых ответственных факторов для определения скороподъемности самолета, в частности как скоро ЛА может подняться на определенную высоту. Вертикальная скорость зависит не от подъемной силы, а от запаса тяги, которым владеет самолет.

Тяга реактивного двигателя самолета

Сила тяги двигателя, либо его движущая сила, равноценна всем силам давления воздуха на внутреннюю поверхность силовой установки. Тяга некоторых видов реактивных двигателей зависит от высоты и скорости полета. Для вычисления силы тяги реактивного двигателя довольно часто приходится определять тягу на конкретной высоте, у почвы, на взлете и на протяжении какой-либо скорости.

Для ЖРД сила тяги равноценна произведению массы исходящих газов на скорость, с которой они вылетают из сопла двигателя.

Для ВРД (воздушно-реактивный двигатель) сила тяги измеряется как следствие массы газов на разность скоростей, в частности скорости воздушной струи, выходящей из сопла двигателя, и скорости поступающего воздуха в двигатель. Несложнее говоря, эта скорость уравнивается к скорости полета самолета с реактивным двигателем. Тяга ВРД в большинстве случаев измеряется в тоннах либо килограммах. Серьёзным качественным показателем ВРД есть его удельная тяга.

Для турбореактивного двигателя – тяга, отнесенная к конкретной единице веса воздуха, что проходит через двигатель в секунду. Данный показатель разрешает осознать, как высока эффективность эксплуатации воздуха в двигателе для образования тяги. Удельная тяга измеряется в килограммах тяги на 1 кг воздуха, расходуемого за секунду.

В некоторых случаях используется второй показатель, что кроме этого именуется удельной тягой, показывающей отношение количества горючего, которое расходуется, к силе тяги за секунду. Конечно, что чем выше показатель удельной тяги ВРД, тем меньше размеры и поперечный вес самого двигателя.

Показатель полетной либо тяговой мощности – это сила, которая задействует реактивный двигатель при конкретной скорости полета. В большинстве случаев, измеряется в лошадиных силах. Величина лобовой тяги говорит о степени конструктивного оптимума реактивного двигателя.

Лобовая тяга – это отношение громаднейшего показателя площади поперечного сечения к тяге. Лобовая тяга равна тяге, в кг поделенной на площадь в метрах квадратных.

Во всемирной авиации самый ценится тот двигатель, что владеет высокой лобовой тягой.

Чем идеальнее ВРД в конструктивном отношении, тем меньший показатель его удельного веса, в частности неспециализированный вес двигателя вместе с обслуживающими агрегатами и приборами, поделенный на величину собственной тяги.

Реактивные двигатели, как и тепловые по большому счету, отличаются друг от друга не только по мощности, весу, другим показателям и тяге. При оценивании ВРД огромную роль играются параметры, каковые зависят от собственной экономичности, в частности от КПД (коэффициент нужного действия). Среди данных показателей главным считается удаленный расход горючего на конкретную единицу тяги.

Он выражается в килограммах горючего, которое расходуется за час на образование одного килограмма тяги.

Увлекательные записи:

Турбовинтовые двигатели употребляются в тех случаях, в то время, когда скорости полета самолета довольно малы. На громадном количестве современных…

Реактивный двигатель самолета — двигатель, создающий нужную для перемещения силу тяги при помощи преобразования внутренней энергии горючего в…

Реверс – механизм для направления части реактивной либо воздушной струи по направлению перемещения создания и воздушного судна обратной тяги. Кроме…

Известны следующие главные типы реактивных двигателей: ракетные, пороховой, жидкостной ракетный; воздушно-реактивные двигатели, прямоточный…

Реактивный двигатель – силовой агрегат, что формирует требуемое для полета самолета тяговое упрочнение посредством изменения внутренней энергии горючего…

Реактивный двигатель – устройство, создающее требуемую для перемещения силу тяги, преобразовывая внутреннюю энергию горючего в кинетическую энергию…

Источник

Время проверки

Тяга (авиация)

Тяга (англ. thrust ) — сила, которая вырабатывается двигателями и толкает самолёт сквозь воздушную среду. Тяге противостоит лобовое сопротивление. В установившемся прямолинейном горизонтальном полёте они приблизительно равны. Если пилот увеличивает тягу, добавляя обороты двигателей, и сохраняет постоянной высоту, тяга превосходит сопротивление воздуха. Самолёт при этом ускоряется. Довольно быстро сопротивление увеличивается и вновь уравнивает тягу. Самолёт стабилизируется на постоянной, но более высокой скорости. Тяга — важнейший фактор для определения скороподъёмности самолёта (как быстро он может набирать высоту). Вертикальная скорость набора высоты зависит не от величины подъёмной силы, а от того, какой запас тяги имеет самолёт.

Дозвуковые ПВРД

Эта группа двигателей предназначена для обеспечения полетов на скоростях, равных от 0,5 до 1,0 числа Маха. Сжатие воздуха и торможение в таких двигателях происходит в диффузоре – расширяющемся канале устройства на входе потока.

Данные двигатели имеют крайне низкую эффективность. При полетах на скорости М= 0,5 уровень увеличения давления в них равен 1,186, из-за чего идеальный термический КПД для них – всего 4,76%, а если еще и учитывать потери в реальном двигателе, эта величина будет приближаться к нулю. Это значит, что при полетах на скоростях M<0,5 дозвуковой ПВРД неработоспособен.

Но даже на предельной скорости для дозвукового диапазона при М=1 уровень увеличения давления равен 1,89, а идеальный термический коэффициент – всего 16, 7%. Эти показатели в 1,5 раза меньше, чем у поршневых двигателей внутреннего сгорания, и в 2 раза меньше, нежели у газотурбинных двигателей. Газотурбинные и поршневые двигатели к тому же эффективны для использования при работе в стационарном положении. Поэтому прямоточные дозвуковые двигатели в сравнении с другими авиационными двигателями оказались неконкурентоспособными и в настоящее время серийно не выпускаются.